• Purpose

• Bagging vs Boosting

  • Bagging
  • Boosting
• Question
• Weak Learners
• Question

• AdaBoost

  • Steps

    • Question
  • Amount of Say
  • Change of Weight

  • Normalized Weights

    • Question
  • Resampling Data

  • Prediction

    • Question
  • Algorithm

• Question

  • Tip
• Summary

• Gradient Boosting

  • GBM Regression

    • Steps
    • Question

  • GBM Classification

    • Question

• XGBoost - Extreme Gradient Descent

  • Steps

    • Question

  • Hyperparameters - Learning Rate, Number of Trees and Subsampling

    • $λ_t$ - the learning rate
    • Subsampling
    • $\gamma$ - Gamma
• Questions
• References

Purpose

Notes on Boosting

Bagging vs Boosting

For a machine learning task (classification or regression), you need a model that identifies the necessary patterns in the data and does not overfit. In other words, ‘the models should not be so simple as to not be able to identify even the important patterns present in the data; on the other hand, they should not be so complex as to even learn the noise present in the data set’.

This solution can be arrived at either through a single model or an ensemble, i.e., a collection of models. By combining several models, ensemble learning methods create a strong learner, thus reducing the bias and/or variance of the individual models.

Bagging

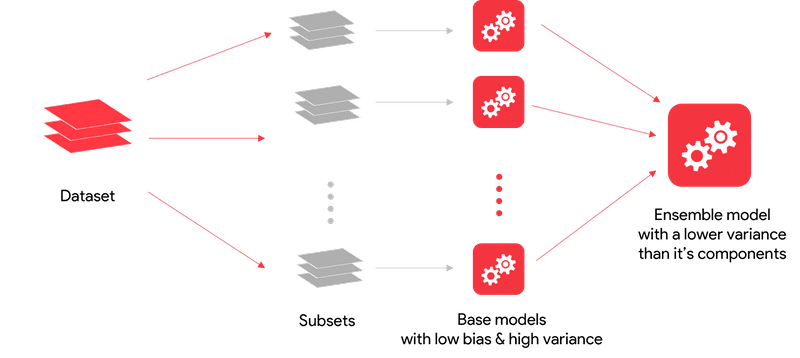
Bagging is one such ensemble model which creates different training subsets from the training data with replacement. Then, an algorithm with the same set of hyperparameters is built on these different subsets of data.

In this way, the same algorithm with a similar set of hyperparameters is exposed to different subsets of the training data, resulting in a slight difference between the individual models. The predictions of these individual models are combined by taking the average of all the values for regression or a majority vote for a classification problem. Random forest is an example of the bagging method.

Bagging works well when the algorithm used to build our model has high variance. This means the model built changes a lot even with slight changes in the data. As a result, these algorithms overfit easily if not controlled. Recall that decision trees are prone to overfitting if the hyperparameters are not tuned well. Bagging works very well for high-variance models like decision trees.

Boosting

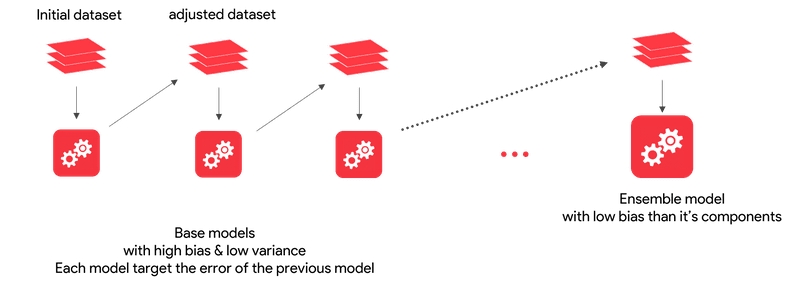
Boosting is another popular approach to ensembling. This technique combines individual models into a strong learner by creating sequential models such that the final model has a higher accuracy than the individual models. Let’s understand this.

These individual models are connected in such a way that the subsequent models are dependent on errors of the previous model and each subsequent model tries to correct the errors of the previous models.

Question

With respect to base models in Ensemble learning, which of the following statements is/are true?

Statement	T/F
In boosting the base models are parallelly connected to reduce the overall bias of the resulting strong model.	F
In bagging the base models are sequentially connected to reduce the overall variance of the resulting strong model.	F
In boosting the base models are sequentially connected to reduce the overall bias of the resulting strong model.	T

Weak Learners

Boosting is an approach where the individual models are connected in such a way that they correct the mistakes made by the previous models. Here, these individual models are called weak learners.

• refers to a simple model which performs at least better than a random guesser
• the error rate should be lesser than 0.5
• primarily identifies only the prominent pattern(s) present in the data
• not capable of overfitting

In boosting, any model can be a weak learner – linear regression, decision tree or any other model, but more often than not, tree methods are used here. Ex: Decision stump is one such weak learner when talking about a shallow decision tree having a depth of only 1.

• combine sequentially such that each subsequent model corrects the mistakes of the previous model, resulting in a strong overall model that gives good predictions.
• Reduce the variance of the final model, making it more robust (generalisable)
• Train the ensemble quickly resulting in faster computation time

Question

Boosting uses weak learners as classifiers because

Statement	T/F
The error is greater than 0.5	F
The error is lesser than 0.5	T
Each weak learner is independent of the previous model	F
Each weak learner is dependent on the previous model	T

AdaBoost

AdaBoost stands for adaptive boosting and was developed by Schapire and Freund.

Steps

• AdaBoost starts with a uniform distribution of weights over training examples, i.e., it gives equal weights to all its observations. These weights tell the importance of each datapoint being considered.
• We start with a single weak learner to make the initial predictions.
• Once the initial predictions are made, patterns which were not captured by the previous weak learner are taken care of by the next weak learner by giving more weightage to the misclassified datapoints.
• Apart from giving weightage to each observation, the model also gives weightage to each weak learner. More the error in the weak learner, lesser is the weightage given to it. This helps when the ensembled model makes final predictions.
• After getting the two weights for the observations and the individual weak learners, the next weak learner in the sequence trains on the resampled data (data sampled according to the weights) to make the next prediction.
• The model will iteratively continue the steps mentioned above for a pre-specified number of weak learners.
• In the end, you need to take a weighted sum of the predictions from all these weak learners to get an overall strong learner.

Question

How do we calculate the final model in the Adaboost algorithm?

• The final model is the weighted sum of the predictions from all these weak learners to get an overall strong learner.
• The final model tries to give importance to each weak learner depending on the error it made in predicting all the samples. So the final model is a weighted sum of all the weak learners

How do we find the variable which will become the root node for the decision tree?

• The variable having the highest Gini score is chosen as the root node.

  • Gini score = 1- Gini impurity. Therefore the higher the Gini impurity the lower is the score.

• The variable having the lowest Gini impurity is chosen as the root node.

  • Gini impurity is a measure of misclassification for a node. Lower the Gini Impurity, higher is the homogeneity of the node. For a pure node(i.e they belong to the same class), the Gini Impurity will be zero.

Amount of Say

In AdaBoost, we start with a base model with equal weights given to every observation. In the next step, the observations which are incorrectly classified will be given a higher weight so that when a new weak learner is trained, it will give more attention to these misclassified observations.

In the end, you get a series of models that have a different say according to the predictions each weak model has made. If the model performs poorly and makes many incorrect predictions, it is given less importance, whereas if the model performs well and makes correct predictions most of the time, it is given more importance in the overall model.

The say/importance each weak learner has in the final classification depends on the total error it made.

$\alpha = 0.5\ln\frac{(1-\text{Total Error})}{\text{Total Error}}$

$\displaystyle \alpha \uparrow \implies \text{Error} \downarrow$

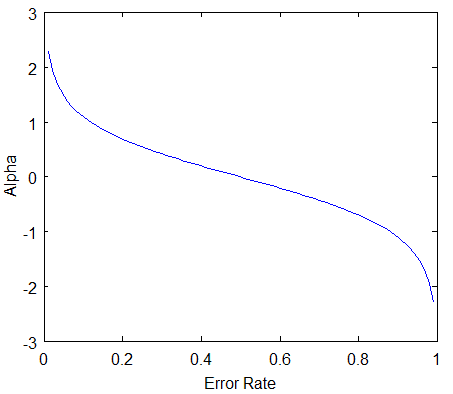
The value of the error rate lies between 0 and 1. So, let’s see how alpha and error is related.

• When the base model performs with less error overall, then, as you can see in the plot above, the α is a large positive value, which means that the weak learner will have a high say in the final model.
• If the error is 0.5, it means that it is not sure of the decision, then the α = 0, i.e., the weak learner will have no say or significance in the final model.
• If the model produces large errors (i.e., close to 1), then α is a large negative value, meaning that the predictions it makes are incorrect most of the time. Hence, this weak learner will have a very low say in the final model.

Change of Weight

• The inital sample weight is same for all the data points for the first weak learner
• For subsequent learners,

Correct Prediction	Incorrect Prediction
$\text{old weight} * e^{-\alpha}$	$\text{old weight} * e^{\alpha}$

Normalized Weights

$\displaystyle \text{Normalized Weight} = \frac{p(x_{i})}{\sum_{i=1}^{N}p(x_{i})}$

Question

After each weak learner has been built and done their prediction, the weights of each sample are modified by a multiplicative factor, according to the total misclassification the weak learner has made.

• The multiplicative factor is a growing weight for all the misclassified samples, therefore they will be given more importance next time.
• The multiplicative factor is a decaying weight for all the correctly classified samples, therefore they will be given less importance next time.

Resampling Data

• Once we have identified the weights for each of the samples, we then resample the data by randomly selecting the data points from a range of values.
• For incorrectly classified values, the range of selection (within the random range of 0-1) will be higher
• This ensures that more number of incorrectly classified data points are selected
• Whenever we start with a new model all the samples of the dataset need to have equal distribution (1/n) and of the same size.
• Also, the new learner should focus more on the samples which are incorrectly classified at the previous iteration.

To handle both these bottlenecks, a new dataset will be created by randomly sampling the weighted observations.

We create a new and empty dataset that is the same size as the original one. Then we take the distribution of all the updated weights created by our first model. You can see the visualisation of the weights below.

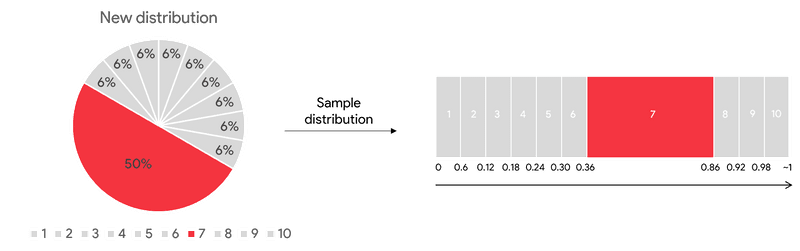
To fill our new empty dataset, we select numbers between 0 and 1 at random. The position where the random number falls determine which observation we place in our new dataset.

Due to the weights given to each observation, the new data set will have a tendency to contain multiple copies of the observation(s) that were misclassified by the previous tree and may not contain all observations which were correctly classified.

After doing this, the initial weights for each observation will be 1/n, thus we can continue the same process as learnt earlier to build the next weak learner.

This will help the next weak learner give more importance to the incorrectly classified sample so that it can correct the mistake and correctly classify it now. This process will be repeated till a pre-specified number of trees are built, i.e., the ensemble is built.

Prediction

The AdaBoost model makes predictions by having each tree in the ensemble classify the sample. Then, the trees are split into groups according to their decisions. For each group, the significance of every tree inside the group is added up. The final prediction made by the ensemble as a whole is determined by the sign of the weighted sum. The final model is a strong learner made by the weighted sum of all the individual weak learners.

Question

Suppose you are performing a binary classification using Adaboost. There are total of 10 samples and the first tree that the model predicted has 2 misclassifications.With this understanding, what will be the say/importance of this tree

• $0.5*\ln((1-0.2)/0.2) = 0.693$

What will be the total updated weights of all incorrect predictions?

• The new weights of incorrect predictions = $2*0.1 * e^{0.693} = 0.399$

Algorithm

1. Initialize the probabilities of the distribution as $\frac{1}{n}$ where n is the number of data points

2. For t=0 to T, repeat the following (T is the total number of trees):

   1. Fit a tree $h_t$ on the training data using the respective probabilities
   2. Compute $\epsilon_t = \sum_{i=1}^{N}D_{i}[h_t(x_{i}) \neq y_{i}]$
   3. Compute $\alpha_t = \frac{1}{2}\ln(\frac{1-\epsilon_t}{\epsilon_t})$
   4. Update $\displaystyle D_{t+1}(i) = \frac{D_t(i)*e^{-\alpha_ty_ih_t(x_{i})}}{z_t} where, z_t = \sum_{i=1}^{N}D_i*e^{-\alpha_ty_{i}h_t(x_{i})}$
3. Final Model: $\displaystyle H(x) = sign(\sum_{t=1}^{T}\alpha_th_t(x))$

You can see here that with each new weak learner, the distribution of the data changes, i.e., the weight given to each observation changes.

• Observe the factor: $\displaystyle e^{-\alpha_ty_{i}h_t(x_{i})}$
• If there is a misclassification done by the model, then the product of $y_{i}*h_t(x_{i})=-1$
• So, the power of the exponential will be positive (growing exponential weight). This indicates that the weight will increase for all misclassified points.
• Otherwise, if it is correctly classified, then a product of $\displaystyle y_{i}*h_t(x_{i}) = 1$
• So, it will have a decaying weight because of the negative term in the power of the exponential term. This indicates that the weight will decrease for all correctly classified points.
• The point here is to force classifiers (weak learners) to concentrate on observations that are difficult to classify correctly.

Question

Why is the error $ϵ_t$ always less than 1/2 in AdaBoost?

• The models used in Adaboost are weak learners but the prediction error they make is less than a random guess. A random guess error is 50% or 0.5. Hence, $ϵ_t$ < $0.5$

Tip

Before you apply the AdaBoost algorithm, you should remove the Outliers. Since AdaBoost tends to boost up the probabilities of misclassified points and there is a high chance that outliers will be misclassified, it will keep increasing the probability associated with the outliers and make the progress difficult. Some of the ways to identify outliers are:

• Boxplots
• Cook's distance
• Z-score.

# scikit-learn has an implementation of adaboost ml model from sklearn.ensemble import AdaBoostClassifier adaboost = AdaBoostClassifier(n_estimators=200, random_state=1) adaboost.fit(X_train, y_train) y_pred = adaboost.predict(X_test)

Summary

• AdaBoost starts with a uniform distribution of weights over training examples.
• These weights give the importance of the datapoint being considered.
• You will first start with a weak learner h1(x) to create the initial prediction.
• Patterns which are not captured by previous models become the goal for the next model by giving more weightage.
• The next model (weak learner) trains on this resampled data to create the next prediction.
• This process will be repeated till a pre-specified number of trees/models are built.
• In the end, we take a weighted sum of all the weak classifiers to make a strong classifier.

---

Gradient Boosting

GBM Regression

Gradient Boosting, like AdaBoost, trains many models in a gradual, additive and sequential manner. However, the major difference between the two is how they identify and handle the shortcomings of weak learners. In AdaBoost, more weight is given to the datapoints which are misclassified/wrongly predicted earlier. Gradient Boosting performs the same by using gradients in the loss function.

• The first prediction in Gradient Boosting for all samples is the average of all the target values.
• Then calculate residulas (average / first prediction - original target value)
• Construct the model (decision tree) on top residulas in which every leaf will contain a prediction of the residual.
• Compute predictions
• Compute new residuals
• Repeat the process with new added trees
• Use all the sequential trees created in the ensemble to make a final prediction

$F_{t+1} = Ft + \lambda h_{t+1}$

Steps

• Build the first weak learner using a sample from the training data; you can consider a decision tree as the weak learner or the base model. It may not necessarily be a stump, can grow a bigger tree but will still be weak, i.e., still not be fully grown.
• Then, predictions are made on the training data using the decision tree which was just built.
• The negative gradient, in our case the residuals, are computed and these residuals are the new response or target values for the next weak learner.
• A new weak learner is built with the residuals as the target values and a sample of observations from the original training data.
• Add the predictions obtained from the current weak learner to the predictions obtained from all the previous weak learners. The predictions obtained at each step are multiplied by the learning rate so that no single model makes a huge contribution to the ensemble thereby avoiding overfitting. Essentially, with the addition of each weak learner, the model takes a very small step in the right direction.
• The next weak learner fits on the residuals obtained till now and these steps are repeated, either for a pre-specified number of weak learners or if the model starts overfitting, i.e., it starts to capture the niche patterns of the training data.
• GBM makes the final prediction by simply adding up the predictions from all the weak learners (multiplied by the learning rate).

To summarize,

• Find the residual and fit a new model on the residual
• Add the new model to the older model and continue the next iteration

Question

What is the reason for introducing the learning rate in GBM?

• To handle overfitting
• The final model is a weighted aggregation of all the individual models we have built in GBM.
• With each additional model, our prediction is getting better and close to the real/target value.
• We do not want any single weak learner to make a big contribution to the overall model which may result in overfitting.
• Learning rate helps us in controlling the contribution of each of the weak learners.
• Without it, the model may suffer from overfitting.

GBM Classification

1. Build the first weak learner using a sample from the training data. Calculate the initial predicition for every individual -> $\ln(odds)$

   • $\displaystyle \ln(odds)\frac{\text{positive class}}{\text{negative class}}$
   • $\displaystyle \text{logistic function (sigmoid)} = \frac{e^{\ln(odds)}}{1+e^{\ln(odds)}}$
2. Calculate the residuals for every sample in the dataset, which will be the new response or target for the next weak learner

3. A new weak learner is built with the residuals as the target values and a sample of observations from the original training data. Constuct the model on top of residuals

   • Output of leaf = $\displaystyle \frac{\sum(Residual)}{\sum[(\text{previous probability}(y_{i})*(1-\text{previous probability}(y_{i})))]}$

4. Compute the predictions

   • New log(odds) = initial log(odds) + LR(output value by D.T)
   • apply logistic function to get probability
5. Repeat process till required number of trees have been built
6. Use all of the trees in the ensemble to make a final prediction
7. The final prediction is adding the current predictions to the predictions obtained from all the previous weak learners. The predictions obtained at each step are multiplied by the learning rate so that no single model makes a huge contribution to the ensemble thereby avoiding overfitting. Essentially, with the addition of each weak learner, the model takes a very small step in the right direction.

Question

Consider that there are total of 6 samples in our dataset for predicting the chances of surviving the ship Titanic. The target value has a binary distribution with 4:2 (surviving:non-surviving) ratio. As part of the first step in the GBM algorithm, we will be starting off with an initial prediction which will be common for all samples. What will be the value of that initial prediction for surviving done by the base model? Round off the values to one decimal.

• 0.7 by using formula: $\frac{e^{\ln(odds)}}{1+e^{\ln(odds)}}$

---

XGBoost - Extreme Gradient Descent

• similar to gradient boosting framework but more efficient and advanced implementation of the Gradient Boosting algorithm.
• First developed by Tainqi Chen and became popular in solving the Higgs Boson problem. Due to its robust accuracy, it has been widely used in machine learning competitions as well.
• supports Regularization
• higher (second) order derivative to optimize loss function
• parallel computing
• missing value handling
• tree pruning using depth first approach

Steps

1. Perform initial prediction and calculate residuals

2. Create a XGBoost Regression Tree

   • Split such as similar residuals should go to same leaf node
   • Create a weak leaner (DT) with a root node consisting of all the residual values and calculate it's similarity score

   • Calculate the similarity score for each node from its first tree split

     • Similarity Score = $\frac{\text{Square of sum of residuals}}{\text{number of residuals} + \lambda}$
     • When values of the residual are very different, the values will cancel out and the similarity score will be low (ex: $\frac{+7.5-7.5}{2} = 0$)
     • Similarity score will be high when # of residual = 1
   • Calculate the gain
   • Gain = Similarity score(Left leaf) + Similarity score(right leaf) - Similarity score (root node)
3. Select the best gain

4. Split the tree further and select the best gain

   • Stop when there is only one residual or some user defined criterion is met

5. Regularisation

   • Tree pruning prevents overfitting with the help of threshold parameter $\gamma$
   • A branch containing the terminal node i pruned when gain < $\gamma$ (or gain-$\gamma$ = negative)
   • If gain-$\gamma$ > 0 => split further else prune
   • In Similarity Score = $\frac{\text{Square of sum of residuals}}{\text{number of residuals} + \lambda}$, increasing the $\lambda$ value will reduce similarity score and hence regularization will take place
6. Calculate Output Value
7. Output Value = $\frac{\text{Sum of Residuals}}{\text{Number of Residuals} + \lambda}$

8. Calculate the final prediction

   • Final prediction = Initial Prediction + L.R(Output Value)
9. Continue the steps till we reach a very small residual value or max no of iterations

Question

Suppose we are building a decision tree using XGBoost with a gamma( γ) of 80. For a depth of 2, we have 3 options for splitting the nodes based on a different threshold. Option 1 will lead to a gain of 108.5, option 2 will lead to a gain of 58 while the last option will lead to a gain of 78. Among the three options which will be chosen for the next split in our decision tree.

• Option 1. A node is further split only if gain-γ > 0

Effect of $\gamma$ and $\lambda$ on XGBoost

• $\lambda \uparrow \implies \text{Regularisation}\uparrow \text{Output Value}\downarrow$
• $\gamma \uparrow \implies \text{Regularisation}\uparrow \text{Number of Leaves}\downarrow$

Hyperparameters - Learning Rate, Number of Trees and Subsampling

$λ_t$ - the learning rate

• is also known as shrinkage.
• It can be used to regularize the gradient tree boosting algorithm.
• $λ_t$ typically varies from 0 to 1.
• Smaller values of $λ_t$ lead to a larger number of trees T (called n_estimators in the Python package XGBoost).
• This is because, with a slower learning rate, you need a larger number of trees to reach the minima.
• This, in turn, leads to longer training time.
• On the other hand, if $λ_t$ is large, we may reach the same point with a lesser number of trees (n_estimators), but there is the risk of actually missing the minima altogether (i.e., cross over it) because of the long stride taken at each iteration.
• Some other ways of regularisation are explicitly specifying the number of trees T and doing subsampling.
• Note that you should not tune both $λ_t$ and number of trees T together since a high $λ_t$ implies a low value of T and vice-versa.

Subsampling

• is training the model in each iteration on a fraction of data (similar to how random forests build each tree).
• A typical value of subsampling is 0.5 while it ranges from 0 to 1.
• In random forests, subsampling is critical to ensure diversity among the trees, since otherwise, all the trees will start with the same training data and therefore look similar.
• This is not a big problem in boosting since each tree is any way built on the residual and gets a significantly different objective function than the previous one.

$\gamma$ - Gamma

• It is a parameter used to control the pruning of the tree.
• A node is split only when the resulting split gives a positive reduction in the loss function.
• Gamma specifies the minimum loss reduction required to make a split and makes the algorithm conservative.
• The values can vary depending on the loss function and should be tuned.

from sklearn.ensemble import GradientBoostingClassifier from sklearn.metrics import accuracy_score xgb_cfl = xgb.XGBClassifier(n_jobs = -1,objective = 'binary:logistic') xgb_cfl.get_params() xgb_cfl.fit(train, target_train) # default xgb_predictions = xgb_cfl.predict(test) accuracy_score(target_test, xgb_predictions) from sklearn.model_selection import RandomizedSearchCV # A parameter grid for XGBoost params = { 'n_estimators' : [100, 200, 500, 750], # no of trees 'learning_rate' : [0.01, 0.02, 0.05, 0.1, 0.25], # eta 'min_child_weight': [1, 5, 7, 10], 'gamma': [0.1, 0.5, 1, 1.5, 5], 'subsample': [0.6, 0.8, 1.0], 'colsample_bytree': [0.6, 0.8, 1.0], 'max_depth': [3, 4, 5, 10, 12] } folds = 5 param_comb = 800 random_search = RandomizedSearchCV(xgb_cfl, param_distributions=params, n_iter=param_comb, scoring='accuracy', n_jobs=-1, cv=5, verbose=3, random_state=42) random_search.fit(train, target_train) print('\n Best estimator:') print(random_search.best_estimator_) print('\n Best accuracy for %d-fold search with %d parameter combinations:' % (folds, param_comb)) print(random_search.best_score_ ) print('\n Best hyperparameters:') print(random_search.best_params_) xgb_predictions_hpt = random_search.predict(test) accuracy_score(target_test, xgb_predictions_hpt)

Questions

Statement	T/F
In GBM, At each iteration, we add an incremental model, which is fitted on the positive gradients of the loss function evaluated at current target values.	False (Calculation is done on Negative Gradients)
In XGBoost, We multiply $λ_t$ (learning rate) with the incremental model h t + 1 so that the new model does not overfit.	True
In Adaboost, The classifier weight grows exponentially as the error approaches 0. Better classifiers are given exponentially more weight.	True
In Adaboost, The classifier weight grows exponentially as the error approaches 0. Better classifiers are given exponentially more weight.	False (at 50% $\alpha = 0$)
In Adaboost, The classifier weight grows exponentially negative as the error approaches 1. These types of classifiers are given a negative weight.	True

For a gradient boosting algorithm, let's say $F_0$ is the crude model with which we start off. For a model Ft which is fitted on the training data, the prediction we get for xi is Ft(xi). What is the general expression of the residuals generated once the Ft model is trained? Assume y is the initial target variable.

• $y - [Fo(xi)+F1(xi) + F2 (xi)+.........+ Ft−2(xi) + Ft−1(xi) + Ft(xi)]$
• The residuals created by F1 is y−F0(xi)−F1(xi), for F2 it is y−F0(xi)−F1(xi) - F2(xi) and so on. In general, Ft trains on the residuals generated by the model Ft−1. So the residuals created by Ft is y - [Fo(xi)+F1(xi) + F2 (xi)+.........+ Ft−2(xi) + Ft−1(xi) + Ft(xi)].

References

• A short introduction to boosting
• Adaboost Regressor Documentation
• Gradient Boosting - StatQuest
• Gradient Boosting - Classification (sklearn)
• Gradient Boosting - Regressor (sklearn)
• XGBoost is not black magic
• XGBoost - Paper
• XGBoost - StatQuest