Decision Trees
- Purpose
- About Decision Trees
- Question
- Advantages of Decision Trees
- Questions
- Summary
- Takeaways
- Question
- Algorithms for Decision Tree
- Questions
- Steps for Selecting Best Split Feature
- Summary
- Questions
- Takeaways
- Questions
- References
Purpose
Notes on Tree based models
About Decision Trees
- With high interpretability and an intuitive algorithm, decision trees mimic the human decision-making process and are efficient in dealing with categorical data. Unlike other algorithms, such as logistic regression and support vector machines (SVMs), decision trees do not help in finding a linear relationship between the independent variable and the target variable. However, they can be used to model highly non-linear data.
- A decision tree, as the term suggests, uses a tree-like model to make predictions. It resembles an upside-down tree and uses a similar process that you do to make decisions in real life, i.e., by asking a series of questions to arrive at a decision.
- A decision tree splits data into multiple sets of data. Each of these sets is then further split into subsets to arrive at a decision.
- It forms the base for Random Forest Classification Algorithm.
- A decision tree uses a natural decision-making process, i.e., it asks a series of questions in a nested if-then-else structure. On each node, you ask a question to further split the data that is held by the node. If the test passes, you move to the left; otherwise, you move to the right.
- The first and top node of a decision tree is called the root node. The arrows in a decision tree always point away from this node.
- The node that cannot be further classified or split is called the leaf node. The arrows in a decision tree always point towards this node.
- The intermediate nodes between the root and the leaf nodes are called the internal nodes.
- it is easy to interpret a decision tree, and you can almost always identify the various factors that lead to a particular decision. In fact, trees are often underestimated in their ability to relate the predictor variables to their predictions. As a rule of thumb, if interpretability by layman is what you are looking for in a model, then decision trees should be at the top of your list.
- In a decision tree, you start from the top (root node) and traverse left/right according to the result of the condition. Each new condition adds to the previous condition with a logical ‘and’, and you may continue to traverse further until you reach the final condition’s leaf node. A decision is the value (class/quantity) that is assigned to the leaf node.
Building Decision Trees
- Recursive binary splitting/partitioning the data into smaller subsets
- Select the best variable for the split
- Apply the split
- Repeat the process for the subsets obtained
- Continue process until stopping criterion is reached
- Assigning the majority class/average value as the prediction
Top Down
- starting from top with larger data and keep splitting
Greedy
- tries to maximize the immediate effect at a node while splitting
- A small variation in the data can result in a significant change in the decision tree leading to different decisions and results altogether.
- due to this decision tree is called a high variance model i.e. smaller changes in data can significantly change what the tree looks like
- The reason we call the process greedy is because it does not take into account what will happen in the next two or three steps. The entire structure of the tree changes with small variations in the input data. This, in turn, changes the way you split and the final decisions altogether. This means that the process is not holistic in nature, as it only aims to gain an immediate result that is derived after splitting the data at a particular node based on a certain rule of the attribute.
Question
The order of attributes in each side of a decision tree is exactly the same.
- No. The order of attributes in each side of the decision tree does not matter in the process of decision making.
Hyperparmaeters
- Hyperparameter tuning can improve the performance of decision trees to a great extent.
- Hyperparameters are simply the parameters that we pass on to the learning algorithm to control the training of the model i.e. these are the parameters that the user provides and not something that the algorithm learns on its own during the training process.
- Hyperparameters are choices that the algorithm designer makes to ‘tune’ the behaviour of the learning algorithm.
- The choice of hyperparameters, therefore, has a lot of bearing on the final model produced by the learning algorithm.
- The values of hyper-parameters are pre-set. The values of hyper-parameters are independent of the dataset. These values do not change during training.
- Hyper-parameter is not a part of the trained or the final model. The values of model parameters estimated during training are saved with the trained model.
- The hyper-parameter values are used during training to estimate the value of model parameters.
Hyperparameter Tuning
Since hyperparameters can take many values, it is essential for us to determine the optimal values where the model will perform the best. This process of optimising hyperparameters is called hyperparameter tuning.
Difference between Parameter and Hyperparameter
| Parameter | Hyperparameter |
|---|---|
| Estimated during the training with historical data | Values are set before hand |
| It is a part of the model | External to the model |
| The estimated value is saved with the trained model | Not a part of the trained model and hence the values are not saved |
| Dependent on the dataset that the system is trained with | Independent of the dataset |
Advantages of Decision Trees
-
Interpretable
- Trees can be visualised.
- Uses a white box model. If a given situation is observable in a model, the explanation for the condition is easily explained by boolean logic. By constrast, in a black box model (e.g., in an artificial neural network), results may be more difficult to interpret.
-
Versatile
- can handle classification as well regression
- It does not assume anything specific about the nature of the attributes in a data set.
- It can seamlessly handle all kinds of data such as numeric, categorical, strings, Boolean, etc.
- Requires little data preparation.
-
Fast
- conditionally partitioning data
- The cost of using the tree (i.e., predicting data) is logarithmic in the number of data points used to train the tree.
- Handle Multicollinearity better: doesn't have distribution assumptions
-
Scale Invariant
- It does not require normalisation, as it only has to compare the values within an attribute.
-
Identifying complex relationships
- subsets can be created which have different predictions
- work well in certain cases where you cannot fit a single linear relationship between the target and feature variables.
- give us an idea of the relative importance of the explanatory attributes that are used for prediction
- Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model.
- Performs well even if its assumptions are somewhat violated by the true model from which the data were generated.
-
Gives Feature Importance
- higher the node, better the feature
- gini number is visible in the nodes
Disadvantages of Decision Trees
-
Overfitting
- Decision-tree learners can create over-complex trees that do not generalise the data well. This is called overfitting.
- can memorize the entire dataset.
- If allowed to grow with no check on its complexity, a decision tree will keep splitting until it has correctly classified (or rather, mugged up) all the data points in the training set.
- Mechanisms such as pruning, setting the minimum number of samples required at a leaf node or setting the maximum depth of the tree are necessary to avoid this problem.
-
High Variance
- Decision trees can be unstable because small variations in the data might result in a completely different tree being generated.
- Bias is too low, hence the variance will be too high.
- This problem is mitigated by using decision trees within an ensemble.
-
NP Complete
- The problem of learning an optimal decision tree is known to be NP-complete under several aspects of optimality and even for simple concepts.
- Consequently, practical decision-tree learning algorithms are based on heuristic algorithms such as the greedy algorithm where locally optimal decisions are made at each node.
- Such algorithms cannot guarantee to return the globally optimal decision tree.
- This can be mitigated by training multiple trees in an ensemble learner, where the features and samples are randomly sampled with replacement.
-
Biased Analysis
- Decision tree learners create biased trees if some classes dominate
- It is therefore recommended to balance the dataset prior to fitting with the decision tree.
- There are concepts that are hard to learn because decision trees do not express them easily, such as XOR, parity or multiplexer problems.
Regression using Decision Trees
- In regression problems, a decision tree splits the data into multiple subsets.
- The difference between decision tree classification and decision tree regression is that in regression, each leaf represents the average of all the values as the prediction as opposed to a class label in classification trees.
-
For classification problems, the prediction is assigned to a leaf node using majority voting but for regression, it is done by taking the average value. This average is calculated using the following formula:
- where represent the observations in a node
- For example, suppose you are predicting the sales your company will have based on various factors such as marketing, no. of products, etc. Now, if you use a decision tree to solve this problem, and if one of the leaf nodes has, say, 5 data points, 1 Cr, 1.3 Cr, 0.97 Cr, 1.22 Cr, 0.79 Cr. Now, you will just take the average of these five values which comes out to be 1.05 Cr, and that becomes your final prediction.
Questions
What do leaves in regression and classification decision trees contain
-
Leaves in classification contain labels.
- In classification, the target variable is discrete. Hence, each data point in a leaf has an associated class label.
- Leaves in regression contain the average predicted value.
Summary
- Decision trees are easy to interpret, as you can always traverse backwards and identify the various factors that lead to a particular decision.
- A decision tree requires you to perform certain tests on attributes in order to split the data into multiple partitions.
- In classification, each data point in a leaf has a class label associated with it.A
- You cannot use the linear regression model to make predictions when you need to divide the data set into multiple subsets, as each subset has an independent trend corresponding to it. In such cases, you can use the decision tree model to make predictions because it can split the data into multiple subsets and assign average values as the prediction to each set independently.
Takeaways
- decision trees are intuitive to understand just by visualizing the model as they mimic human decision-making process
- they are fast (logarithmic time complexity) because they split data into subsets on each condition
- decision trees are greedy i.e. they only care about what will be the most optimal solution for the current node. They don't care about the global solution optimization
- decision trees can overfit and are know to be susceptible to changes in the data set (i.e they have high variance) as well as class imbalance
Splitting and Homogeneity
- We split the data to get groups which are homogeneous or pure or largely belong to one class.
- We keep splitting till homogeneity exceeds a threshold value after which that node becomes a leaf node.
- homogeneity refers to response (target) variable's homogeneity.
- For classification purposes, a data set is completely homogeneous if it contains only a single class label.
- For regression purposes, a data set is completely homogeneous if its variance is as small as possible
- The goal of decision tree splitting is to increase homogeneity. More homogeneity will mean that most of the data points in the set belong to the same class label. Hence, classifying all the data points of that set, to get them to belong to that class, will result in fewer errors.
CART Algorithm
A tree can be split based on different rules of an attribute and these attributes can be categorical or continuous in nature. If an attribute is nominal categorical, then there are possible splits for this attribute, where k is the number of classes. In this case, each possible subset of categories is examined to determine the best split.
If an attribute is ordinal categorical or continuous in nature with n different values, there are different possible splits for it. Each value of the attribute is sorted from the smallest to the largest and candidate splits based on the individual values is examined to determine the best split point which maximizes the homogeneity at a node.
Discretization
Calculating percentiles and midpoints of the sorted values for handling continuous features is known as discretization
- Refer this article for more information.
Question
Given a dataset with two attributes, age and gender, you want to predict whether a person will purchase a product (yes/no). You know that among all those who have purchased the product in the past, 98% are females. Also, the age distribution of the customers is almost uniform. The homogeneity of the resultant nodes will be maximised if you split on Age or Gender?
- Gender as it will split the data such that one node will contain 98% of total observations that belong to 'product purchased' class and the other node will contain 2% of total observations belonging to 'product purchased' class. So, nodes will have high homogeneity here.
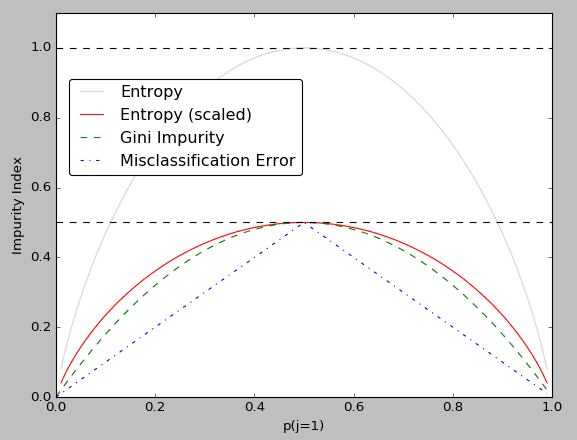
Impurity Measures
- Measures of misclassification of data
- The measures don't distinguish between classes.
Classification Error
- minority becomes the classifcation error if everything is assigned to majority class
- Max ambiguity value is 0.5
Gini Impurity
where , is the probability of finding a point with the label and is the number of classes
Note that because sum of all probabilities is equal to 1
- Min ambiguity (all elements belong to single class) is 0
- Max ambiguity value is 0.5
- most popular impurity index along with being the default in sklearn library
Entropy
- Min ambiguity value is 0
- Max ambiguity value is 1
- Here is assumed to be 0
- Entropy quantifies the degree of disorder in the given data, its value varies from 0 to 1.
Algorithms for Decision Tree
- = Impurity (post split) < Impurity (pre-split)
- Split that does this best is chosen
- The post-split impurity is calculated by finding the weighted average of two child nodes. The split that results in maximum gain is chosen as the best split.
- Information Gain = where is the entropy of the parent set (data before splitting), is the entropy of the partitions obtained after splitting on attribute .
- (reduction in entropy implies information gain)
- In case of a classification problem, you always try to maximise purity gain or reduce the impurity at a node after every split and this process is repeated till you reach the leaf node for the final prediction.
Questions
Considering all the data points in a data set have the same label, what will be the Gini index?
-
- The probability of exactly one class will be 1, and the probability of all the other classes will be 0. So, the Gini index, which is given by , will be 0.
In a given data set, 50% of the data points belong to label 1, and the other 50% belong to label 2. Calculate the Gini index.
- 0.5. Using formula for Gini Index:
Steps for Selecting Best Split Feature
- Calculate the Gini impurity before any split on the whole dataset.
- Consider any one of the available attributes.
- Calculate the Gini impurity after splitting on this attribute for each of the levels of the attribute.
- Combine the Gini impurities of all the levels to get the Gini impurity of the overall attribute.
- Repeat steps 2-5 with another attribute till you have exhausted all of them.
- Compare the decrease in Gini impurity across all attributes and select the one which offers maximum reduction.
Summary
- A decision tree first decides on an attribute to split on.
- To select this attribute, it measures the homogeneity of the nodes before and after the split.
- You can measure homogeneity in various ways with metrics like Gini index and entropy.
- The attribute that results in the increase of homogeneity the most is then selected for splitting.
- Then, this whole cycle is repeated until you obtain a sufficiently homogeneous data set.
Hyperparameter Tuning in Decision Trees
- Decision trees have a tendency to overfit the data. A large tree will have a leafy only to cater to a single data point
- There are two broad ways to control overfitting: truncation and pruning
| Truncation | Pruning |
|---|---|
| Stop the tree while it is still growing so that it may not end up with leaves containing very few data points. Note that truncation is also known as pre-pruning. | Let the tree grow to any complexity. Then, cut the branches of the tree in a bottom-up fashion, starting from the leaves. It is more common to use pruning strategies to avoid overfitting in practical implementations |
| top down | bottom up |
| don't grow further than specified depth or if some criteria is met | delete leaves based on criteria |
| Ex: Homogeneity > Threshold |
Methods of Truncation
- Limit the minimum size of a partition after a split
- Minimize change in the measure of homogenity
- Limit the depth of the tree
- Set a minimum threshold on the number of samples that appear in a leaf
- Set a limit on the maximum number of leavest present in tree
No objective way coming up with the number for the various parameters. It is essentially based on domain knowledge and trial and error.
Hyperparameters in DecisionTeeClassifier
-
max_features: It defines the no. of features to consider when looking for the best split.
- We can input integer, float, string & None value.
- If an integer is inputted then it considers that value as max features at each split.
- If float value is taken then it shows the percentage of features at each split.
- If “auto” or “sqrt” is taken then maxfeatures=sqrt(nfeatures).
- If “log2” is taken then maxfeatures= log2(nfeatures).
- If None, then maxfeatures=nfeatures.
- By default, it takes “None” value.
-
maxdepth: The maxdepth parameter denotes the maximum depth of the tree.
- It can take any integer value or None.
- If None, then nodes are expanded until all leaves contain just one data point (leading to overfitting) or until all leaves contain less than "minsamplessplit" samples.
- By default, it takes “None” value.
-
minsamplessplit: This tells about the minimum no. of samples required to split an internal node.
- If an integer value is taken then consider minsamplessplit as the minimum no.
- If float, then minsamplessplit is a fraction and ceil(minsamplessplit * n_samples) are the minimum number of samples for each split.
- By default, it takes the value "2".
-
minsamplesleaf: The minimum number of samples required to be at a leaf node.
- If an integer value is taken then consider minsamplesleaf as the minimum no.
- If float, then it shows the percentage. By default, it takes the value "1".
How to find best parameters
- we can use K-Fold Cross Validation technique
-
It is implemented in sklearn
Questions
As you increase the value of the hyperparameter minsamplesleaf, the resulting tree will become more complex or less?
- It will become less complex, and the depth will tend to reduce.
- minsamplesleaf is the minimum number of samples required in a (resulting) leaf for the split to happen. Thus, if you specify a high value of minsamplesleaf, the tree will be forced to stop splitting quite early.
Suppose you decide to tweak the hyperparameters so as to decrease the overfitting. Which steps can one follow?
-
Increasing minsamplessplit
- A low value of the minsamplessplit will lead to a small number of data points in the nodes. This means that it is very likely that each leaf (obtained after splitting) is going to represent very few (or only one, in some cases) data points. So, you increase the minsamplessplit.
-
Decreasing max_depth
- Decreasing max_depth will stop the tree to grow deeper, in that way your tree will not overfit the data and you will have a decent accuracy in both test and train.
What will the (likely) impact of increasing the value of minsamplesplits from 5 to 10?
-
The depth will decrease.
- Since the node should now contain at least 10 data points before splitting, as opposed to 5, all the branches — where the nodes had less than 10 data points — will be chopped off, leading to a decrease in the tree depth.
Decision Tree Regression
- In decision tree regression, each leaf represents the average of all the values as the prediction as opposed to taking an majority vote in classification trees.
Prediction
- Average value of the target available in the node
- This is nothing but the sum of all data points divided by the total number of data points.
Impurity Measure
- Weighted Mean Square Error (WMSE) a.ka. variance:
- This is nothing but the variance of all data points.
- A higher value of MSE means that the data values are dispersed widely around mean, and a lower value of MSE means that the data values are dispersed closely around mean and this is usually the preferred case while building a regression tree.
Process
The regression tree building process can be summarised as follows:
- Calculate the MSE of the target variable.
- Split the data set based on different rules obtained from the attributes and calculate the MSE for each of these nodes.
- The resulting MSE is subtracted from the MSE before the split. This result is called the MSE reduction.
- The attribute with the largest MSE reduction is chosen for the decision node.
- The dataset is divided based on the values of the selected attribute. This process is run recursively on the non-leaf branches, until you get significantly low MSE and the node becomes as homogeneous as possible.
- Finally, when no further splitting is required, assign this as the leaf node and calculate the average as the final prediction when the number of instances is more than one at a leaf node.
So, you need to split the data such that the weighted MSE of the partitions obtained after splitting is lower than that obtained with the original or parent data set. In other words, the fit of the model should be as ‘good’ as possible after splitting. As you can see, the process is surprisingly similar to what you did for classification using trees.
Key Insights
-
Leaves in decision tree regression contain average values as the prediction.
- Each leaf in regression contains an average value that is used for prediction.
-
The MSE gives a sense of how good or bad the linear regression fit is.
- The MSE is a measure of the average squared differences between the estimated values and the actual value.
-
Decision tree regression and classification are similar in the sense that both try to pick an attribute (for splitting) that maximises the homogeneity of a data set.
- A decision tree splits a data set on the attribute that results in the maximum increase in homogeneity.
Takeaways
- decision trees are prone to overfitting and have a high variance
- hyperparamerter tuning is required to reduce overfitting. Parameters such as minsamplessplit and minsamplesleaf help in stopping the decision tree to grow in a way that it does not end up memorizing the whole dataset
- decison tree regression and decision tree classification have similar algorithms, where we try to find the best node to split on along with the condition on which to split. The best node is decided by max MSE/Gini reduction compared to parent. Once criteria is met, we stop growth of tree.
Questions
Difference between Random Forest and Decision Tree?
- Decision Tree uses all the features for training while random forest selects a subset of features
Consider decision tree A learned with minsamplesleaf = 500. Now consider decision tree B trained on the same dataset and parameters, except that the minsamplesleaf=50. What can you say about depth, number of samples and training error of the two models?
-
The depth of B >= the depth of A
- minsamplesleaf guarantees a minimum number of samples in a leaf. Higher no of this parameter means you are stopping early. A lower value allows you to grow further.
-
The number of nodes in B >= the number of nodes in A
- minsamplesleaf guarantees a minimum number of samples in a leaf. Higher no of this parameter means you are stopping early. A lower value allows you to grow further. As the tree grows no of nodes increases.
-
The training error of B <= the training error of A
- minsamplesleaf guarantees a minimum number of samples in a leaf. Higher no of this parameter means you are stopping early. A lower value allows you to grow further. As the tree grows no of nodes increases. With more nodes and deeper tree , it tends to memorize training data and variance of the model increases.