Random Variable

• which maps the output of a random experiment to a numerical value
• Radom Experiment Example: tossing a coin

Expected Value

• average value of radom variable in the long run
• $\displaystyle E(x) = \sum_{i=1}^{N}P(x_{i})\times x_{i}$

Probability

• sum of all probabilities in an experiment is equal to 1

Inferential Statistics

• It is difficult to read the behavior of the complete population due to time and cost issue
• We can use inferential statistics where we infer information about population from sample
• Example: Lead content in Maggi Packets

Central Limit Theorem

• Sampling distribution mean is the mean of sample means
• Number of units in every sample is called sample size

• The sampling distribution Mean = Population Mean

  • $\mu_s = \mu_p$
• Standard Error = $\sigma_p = \frac{\mu_s}{\sqrt n}$
• If $n>30$, sammpling distribution is assumed to be normally distributed

Confidence Interval

$\mu \pm \frac{Z^*\sigma}{\sqrt n}$

Hypothesis Testing

• Hypothesis: A claim or an assumption \thetaat we make about one or more population parameters

• Types of Hypothesis:

  • Null Hypothesis ($H_0$)

    • makes an asummption about the status quo
    • always contains the symbols $=, \leq, \geq$

  • Alternate Hypothesis ($H_1$)

    • challenges and complements the null hypothesis
    • always contains the symbols $\neq, <, >$
• $H_0 \& H_1$ are disjoint events

Upper Tailed Test

• The critical region lies on the right side of the distribution
• The alternate hypothesis contains < symbol
• If alpha is 0.5, p-value = 0.95

Lower Tailed Test

• The critical region lies on the left side of the distribution
• The alternate hypothesis contains > symbol
• If alpha is 0.5, p-value = 0.05

Two Tailed Test

• The critical region lies on both sides of the distribution
• The alternate hypothesis contains $\neq$ symbol
• If alpha is 0.5, p-value range (cumulative over sections): [0, 0.025, 50, 0.975, 1]

Exploratory Data Analysis

• Types of Data

  • Public Data: data collected by the government or other public agencies that are made public for the purposes of research are known as Public data
  • Private Data: Data generated by Banking, telecom, retail and media are some examples of private data. This data cannot be used freely for analysis

• Univariate

  • Analyzing one variable at a time
  • historgram, countrplot, boxplot

• Bivariate

  • Analyzing two variables at a time
  • scatterplot, barplot, boxplot, pairplot

• Multivariate

  • Analyzing more than two variables at a time
  • barplot, scatterplot, boxplot
• Outlier Analysis

• Categorical Data

  • discrete values

• Continuous Data

  • range of values

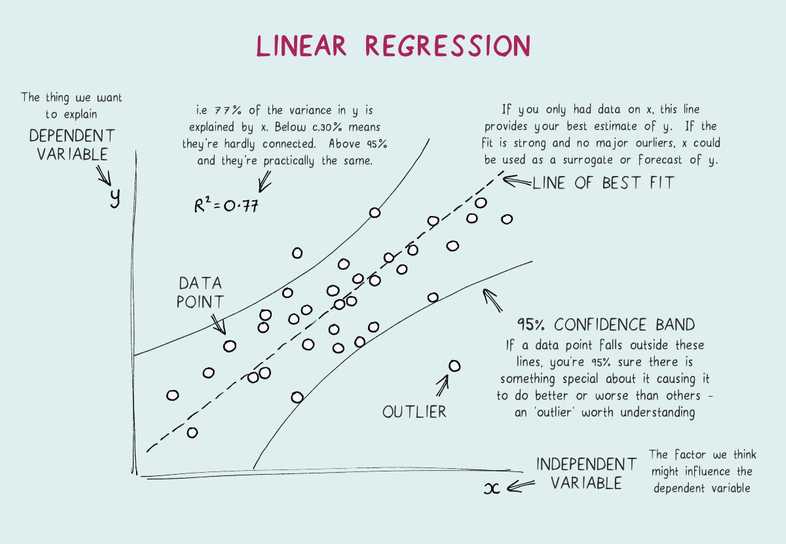
Linear Regression

• It is the simplest form of regression. It is a technique in which the dependent variable is continuous in nature. The relationship between the dependent variable and independent variables is assumed to be linear in nature.
• Simple Linear Regression - one independent variable
• Multiple Linear Regression - more than one independent variable

$R^2$

• Out of total variance how much is explained by the model
• $\displaystyle \frac{1 - RSS}{TSS}$

RSS

• how much target value varies around the regression line
• $\displaystyle Error = \sum_{i=1}^{N}(Actual - Predicted)^2$

Adjusted $R^2$

$Adj R^2 = 1 - \frac{(1-R^2)(N-1)}{(N-P-1)}$

• contains effect of data size
• N = Number of Rows
• P = number of Features

Logistic Regression

• Sigmoid Curve ranges from 0 to 1
• Log Odds = $\displaystyle \ln\frac{P}{1-P} = \beta_0+\beta_1x_{i}$
• Odds = $\displaystyle \frac{P}{1-P}$

Naive Bayes

• based on Bayes theorem
• $\displaystyle P(A|G) = \frac{P(G|A)\times P(A)}{P(G)}$
• $\displaystyle P(y|(x_1,x_2,\ldots,x_n)) = \frac{\prod_{i=1}^{N}P(x_i|y)\times P(y)}{\prod_{i=1}^{N}P(x_i)}$

Important Topics

• Expected Values
• Mean, Median, Mode
• Probability
• CLT
• $H_0, H_1$ hypothesis formulation
• EDA graph based questions
• R^2, Adj R^2, y=mx+c
• odds: $\displaystyle y = \frac{1}{1+e^{-\beta_0+\beta_1x_1}}$
• sigmoid
• recall, precision, specificity, sensitivity, confusion matrix
• precision: out of all the 0s you "PREDICTED" (TP+FP), how many are actually zero (TP)
• recall: out of all the 0s there actually are (TP+FN), how many you predicted correctly (TP)