Purpose

Notes on Naive Bayes Classifier

About

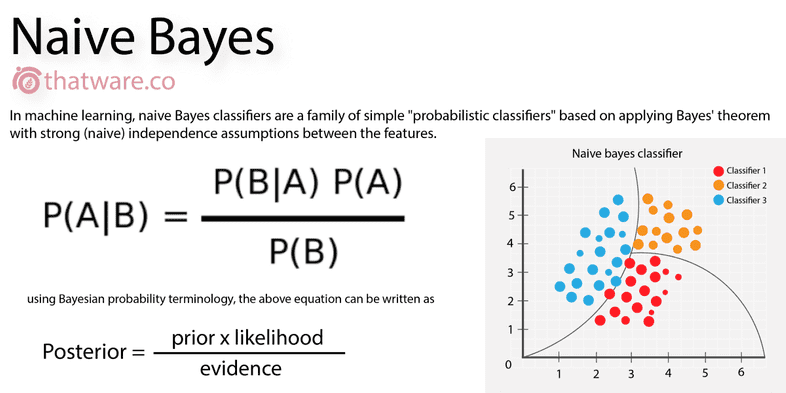
Naive Bayes is a probabilistic classifier which returns the probability of a test point belonging to a class, using Bayes' theorem.

Uses

It is used for text classification such as when identifying whether an email is spam or ham.

Conditional Probability

$Probability = \frac{\text{Number of favorable outcomes}}{\text{Total Number of Outcomes}}$

Prior: Independent probability of an event happening

• Ex: P(Play) = 66% [or P(A)]

Posterior: Probability of an event happening, given some other event has also occurred

• Ex: P(Play|Rain) = 10% [or P(A given B)]

Need for Conditional Probability

Conditional probability is needed to understand relative probabilities, which is more often the case in the real world scenarios instead of looking into the absolute probability of events in isolation.

Bayes Theorem

Two Way Contingency Matrix

B\A	A = Win	A = Loss	Total
B = Century	10	2	12
B = No Century	50	38	88
Total	60	40	100

Here: A means India Win and B means Sachin's Century

$\text{P(A)} = \frac{60}{100}$

$\text{P(B)} = \frac{12}{100}$

Joint Probability

• P(A,B) = Indian Win and Sachin's Century
• $P(A \cap B) = \frac{10}{100} = 10\% = P(B\cap A)$
• $P(A \cap B) = P(A|B).P(B) = P(B|A).P(B)$
• Sample Space Remains Same

Conditional Probability

• India wins, given that Sachin has scored a century
• $\text{P(A|B)} = \frac{10}{12} = 83.3\%$
• $P(A|B) = \frac{10}{12} = \frac{\frac{10}{12}}{\frac{12}{100}} = \frac{P(A \cap B)}{{P{(B)}}}$
• Sample space gets reduced to the number of times the event we are conditioning on occurs

Bayes Theorem

Since, $P(A \cap B) = P(A|B).P(B) = P(B|A).P(B)$

• $\boldsymbol{P(A|B) = \frac{P(B|A).P(A)}{P(B)}}$
• $\boldsymbol{P(B|A) = \frac{P(A|B).P(B)}{P(A)}}$

• The simplest form of Bayes’s rule is in odds form:

  • Posterior odds = Prior odds x Likelihood ratio
  • where the posterior odds are the odds (the ratio of probabilities) for two competing hypotheses.

Note

• Sample Space for Joint Probability remains same while it changes for Conditional probability

Takeaways

• Conditional Probability: It is the probability of an event occurring given some other event has already occurred
• Joint Probability: It is the probability that event A and event B both have occurred
• Bayes Theorem: P(A|B) = P(A)*P(B|A)/P(B) can be derived using a two-way contingency matrix
• Sample Space for Joint Probability remains same while it changes for Conditional probability

---

Principles from Bayes Thinking

1. Remember your priors
2. Imagine your theory's wrong. Would the world look different?
3. Update incrementally (snowflakes of evidence)

MAP - Maximum Aposteriori Classification

• If $P(C_{1}/X) > P(C_{2}/X)$
• X is classified as $C_1$

Naive Bayes Assumption

• Variables are independent given class
• or, variables are conditionally independent
• decreases computation time of the algorithm

Terms used in Naive Bayes Classification

$P(C_i|X = \frac{P(X|C_i)P(C_i)}{P(X)}$

Prior Probability

• $P(C_{i})$
• It is the probability of occurrence of an event before collection of new data or features.
• heavy influence on Bayesian Classification

Likelihood Function

• $P(X|C_i)$
• Maximises probability of observing data
• tells us the likelihood of a data point occurring in a particular class

Denominator

• The effect of the denominator P(x) is not incorporated while calculating probabilities as it is the same for both the classes and hence, can be ignored without affecting the final outcome.

Posterior Probability

• $P(C_i|X)$
• The probability of event occurring after incorporating new evidence in the data

Takeaways

• For classification, we don't need to compute the denominator, we can just compare the numerators for both cases (as the denominator will anyways cancel out) and choose which class the test point belongs to.
• We assume that variables are conditionally independent when implementing Naive Bayes classification
• Prior probability can have large impact on New (Posterior) probability while likelihood function helps in classifying where the test points lies (i.e. in which class)

---

Document Classification

Bag of Words

The sentences are broken down into words and the ordering doesn't matter anymore as if it were put in a bag and shuffled.

Stop Words

These are generic words such as and, the, of, which don't hold any intrinsic values when it comes to classifying documents.

Multinomial Naive Bayes

• If a word from dictionary occurs multiple times in the document, we raise the power of it's probability by that number.
• Suppose that P(great) = 0.1 and P(world) = 0.3 and the document is "great great world", then it's likelihood will be expressed as ${(0.1)}^2*{(0.3)}$.

Zero Probability Problem

While trying to calculate the likelihood of a test document for a given class, it is possible that there exist certain words which although are a part of the dictionary but don't appear in the training documents of that class like the word pepsi does not appear in documents of hot class but it does in cold class. Then, the probability of that word for that class becomes zero ( P(pepsi|hot) =0 ) and it makes the complete likelihood term zero. This is called the zero-probability problem.
To counter this problem, a ‘1’ is added to the total of every word count of all the words of the dictionary for that class. This increases the total word count for that class by the length of the dictionary. This technique is called Laplace Smoothing.

Laplace Smoothing

• Document cannot be classified because probability of one of terms is 0.
• Apply Laplace Smoothing, which adds 1 to all frequencies, hence no term has zero probability
• Prob After Smoothing = $\frac{curr\;frequency + 1}{curr\;total + |v|}$

word	freq	prob	freq after smoothing	prob after smoothing
power	1	1/3	2	2/6
food	0	0	1	1/6
hunger	2	2/3	3	3/6

Note

If there are words occurring in a test sentence which are not a part of the dictionary, then they will not be considered as part of the feature vector since it only considers the words that are part of the dictionary. These new words will be completely ignore.

Bernoulli Naive Bayes

• doesn't care about the frequency of occurrence of a word in the dictionary.
• Bernoulli Naive Bayes is concerned only with whether the word is present or not in a document, whereas Multinomial Naive Bayes counts the no. of occurrences of the words as well.
• Likelihood and Laplace Smoothing are different from Naive Bayes Classifier.

• Likelihood Function:

  • $\displaystyle P(w_1,w_2,\ldots,w_n|C) = P(d|C) = \prod_{n=1}^{|v|}[d_iP(w_i|C)+(1-d_i)(1-P(w_i|C))]$
  • d is the feature vector of document

• Laplace Smoothing:

  • $P(w_t|C) = \frac{n_c(w_t)+1}{N_c+2}$
  • $n_c(w_t)$ is the number of documents in class C in which word $w_t$ is present
  • $N_c$ is the total no of documents in class C

• Binarization of a feature vector

  • Converting all non-zero word count of a feature vector to 1 and leaving zero counts as it is

Determine if two variables are independent

$P(A \cap B) = P(A|B).P(B) = P(A)*P(B)$ must hold true

Model Building Process for Naive Bayes Classifier

1. Load Data
2. Identify target (class) column and map it to numeric values
3. Convert dataset to array using .values()

4. Convert text values to bag of words notation using CountVectorize

   • use stop_words to remove common words such as 'and', 'the' which don't add value for classification

   • use min_df & max_df to limit what frequency of words will be picked

     • Suppose we don't want to consider those (rare) words which have appeared only in 3% of the documents, or say those (extremely common ones) which have appeared in 80% of the documents.
     • CountVectorizer(stopwords='english', mindf=.03, max_df=.8)
5. Fit using vec.fit(X_train) on training set

6. Transform using vec.transform(X_train) on Training as well as Test Set

   • This converts the data to Compressed Spare Row format
   • Note: Do not ever fit on test set, only use transform on test set
7. Build a model on training set

from sklearn.naive_bayes import BernoulliNB # instantiating bernoulli NB class bnb=BernoulliNB() # fitting the model bnb.fit(X_transformed, y_train) # predicting probability of test data prob_bnb = bnb.predict_proba(X_test) prob_bnb # predicting class prob_bnb = bnb.predict(X_test) prob_bnb

8. Analyze model using metrics from sklearn

   • accuracy_score
   • roc_curve, auc
   • confusion matrix
   • precision
   • recall
   • specificity
   • sensitivity
9. Choose model based on business requirement. Some business problems will prefer specificity over sensitivity, others will want the opposite.

Takeaways

1. Naive Bayes Classifier is generally very good for Document classification. Here the documents are converted to bag of words and stop words are removed.
2. Multinomial Naive Bayes considers frequency of occurence of a word, while Bernoulli Naive Bayes only considers whether a word has appeared in the document or not
3. Laplace Smoothing is applied to counter Zero Probability Problem (likelihood function becomes 0 because one of the probabilities is zero)

References

• http://www.malinc.se/math/latex/basiccodeen.php
• https://stats.stackexchange.com/questions/74082/what-is-the-difference-in-bayesian-estimate-and-maximum-likelihood-estimate
• https://tex.stackexchange.com/questions/595/how-can-i-get-bold-math-symbols
• https://cdn.upgrad.com/UpGrad/temp/e3ff7cbe-4892-467f-8869-5eb56b889fda/Worldly%20Wisdom%20in%20an%20Equation.pdf
• https://stackoverflow.com/questions/10059594/a-simple-explanation-of-naive-bayes-classification
• https://math.stackexchange.com/questions/23093/could-someone-explain-conditional-independence
• https://stats.stackexchange.com/questions/105501/understanding-roc-curve