Feed Forward in Neural Networks
Flow of Information in Neural Networks
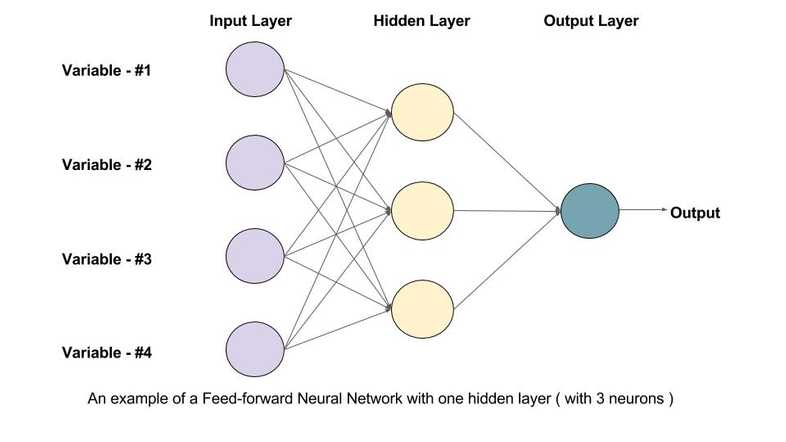
In artificial neural networks, the output from one layer is used as input to the next layer. Such networks are called feedforward neural networks. This means there are no loops in the network - information is always fed forward, never fed back.
Comprehension - Count of Pixels
The figure below shows an artificial neural network which calculates the count of the number of pixels which are ‘on’, i.e. have a value of 1. It further amplifies the output by a factor of 2; so if 2 pixels are on, the output is 4, if 3 pixels are on the output is 6 and so on.
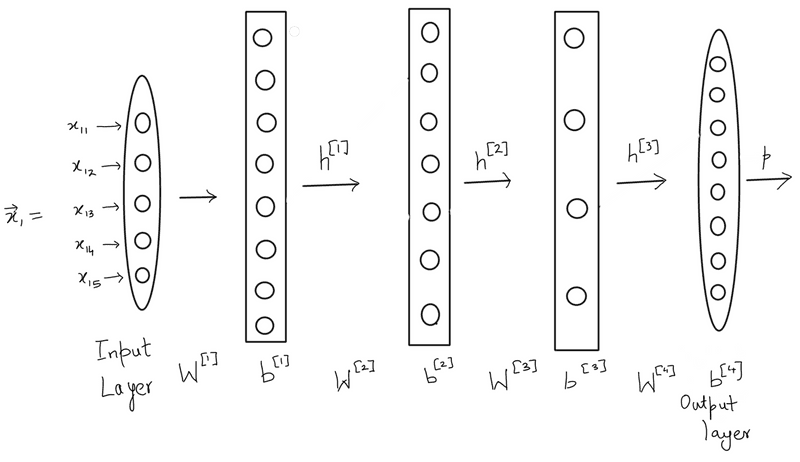
We’ll call the input layer as layer 0 or simply the input layer. The other three layers are numbered 1, 2 and 3 (3 is the output layer).
The weight matrices of the 2 hidden layers and the third output layer are shown above. The first and the second neurons of the (hidden) layer 1 represent the number of ‘on’ pixels in row 1 and 2 respectively. The second (hidden) layer amplifies the output of layer 1 by a factor of 2 and the third (output) layer sums up the amplified counts.
The biases are all 0 and the activation function is
Let's make one minor modification in our network - let’s represent the input with 4 pixels as a vector with pixels counted clockwise. Thus the input shown in the figure is \begin{bmatrix}1\0\0\1\end{bmatrix}
If the output of the network is 6, then the possible inputs are
| Input Matrix | Valid |
|---|---|
| \begin{bmatrix}0\1\1\1\end{bmatrix} | Yes |
| \begin{bmatrix}1\0\1\1\end{bmatrix} | Yes |
| \begin{bmatrix}0\0\1\1\end{bmatrix} | No |
| \begin{bmatrix}1\1\0\1\end{bmatrix} | Yes |
- The on pixels are represented by number 1. It amplifies the output by a factor of 2. So if 3 pixels are on, then output is 6.
For the input , the output of the first neuron of hidden layer 1 is
- 2
- This neuron represents the number of pixels that are on row 1, which is 2
Now, you want to modify the weights of layer-1 so that the first and the second neurons in the hidden layer 1 represent the number of ‘on’ pixels in the first and second column of the input image respectively. This should be true for all possible inputs into the network. What should be ? (note that the input vector is created by counting the pixels clockwise)
- The first neuron’s output will be the first row of w1 multiplied by the input vector.
- If the input vector is [1 0 0 1], i.e both pixels in the first column are on, then the output of neuron 1 should be 2.
- For [1 0 0 0], the output should be 1.
- In general, for the first neuron, the output should sum up the first and the fourth element of the input.
- Thus row 1 should be [1 0 0 1].
- Similarly, for the second neuron, the output should sum up the second and the third element of the input. So the second row should be [ 0 1 1 0].
Let's assume that each elementary algebraic operation, such as multiplication of two numbers, applying the activation function on a scalar f(x), etc. takes 0.10 microseconds (on a certain OS in python). Note that addition is NOT included as an operation. For the network discussed above, how much time would it take to compute the output from the input given all the parameters?
Hint: There are 3 weight matrices of sizes . The activation function is applied to each of the three layers' input to compute .
- 1.9 microseconds
-
Layer 1
- For the weight matrix : It is a (2\times 4)(4\times 1) product, thus has 8 multiplications (one for each row).
- The activation function is then applied to the 2 neurons.
- Thus 10 x 0.1 ms is the time taken till layer 1's output
-
Layer 2
- For layer 2, , it is a 2 x 2 product + activation function applied on 2 scalars.
- So far, we have 8 + 2 + 4 + 2 = 16 operations
-
Layer 3
- For layer 3, its a (2x1)(1x2) matrix product + 1 activation operation
- Thus, we have 16 + 3 = 19 operations which will take 1.9 microseconds
Dimensions in a Neural Network
Input Vector
- The input vector dimensions are just the number of features times 1 making it a column vector.
- Ex: (5, 1) or (5, ) is an input vector, while (5, 5) or (1, 5) is not.
- Note that by default vectors are assumed to be column vectors unless state otherwise.
Weight Matrix
- The weights are always in a matrix form.
- Ex: (5, 5) or (3, 5) or (7, 2) are valid dimensions for weight matrices
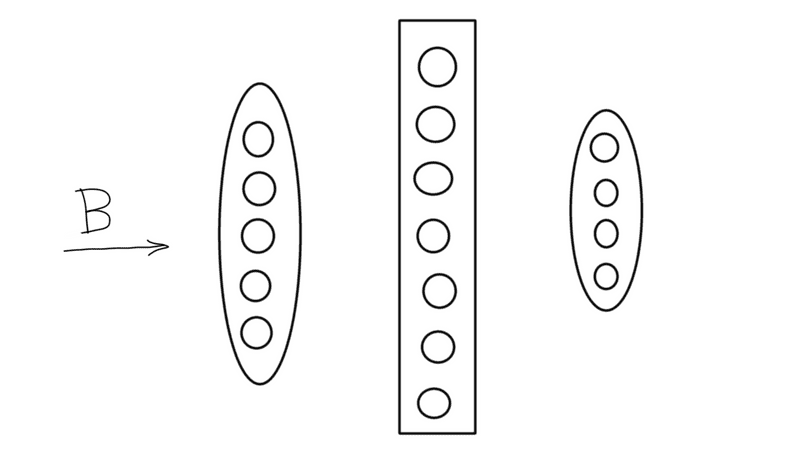
- Note that the weight matrix should have column dimension same as the input vector it is going to receive since we take the dot product of the weight matrix () with input vector () as follows:
M.v. - As per the rules of matrix multiplication, if Matrix has dimension while B has dimensions then their dot product can only be taken if
Example
Dimension of input vector
- (5, 1)
- There are 5 neurons in the input layer. Hence (5,1). By default, a vector is assumed to be a column vector.
Dimensions of
- The dimensions of are defined as (number of neurons in layer l, number of neurons in layer l-1)
Dimensions of the output vectors of the hidden layers and
- The dimension of the output vector for a layer l is (number of neurons in the layer, 1)
The dimension of the bias vector is the same as the output vector for a layer l for a single input vector. True or False.
- True
What is the number of learnable parameters in this network? Note that the learnable parameters are weights and biases.
- 183
- The weights have 40, 56, 28, 32 individual parameters(the weight elements). The layers have 8, 7, 4, 8 biases respectively.
Output
Output of a layer
-
Weight matrix of layer l is multiplied by hidden layer l-1's output (input vector if it's first output we are considering)
-
Add bias
-
Apply activation function
Elaborating on Dimensions
Say, dimension of and dimension of ,
then weight matrix will be of the dimension
You can try with multiplying two matrices and checking their dimensions to understand why that must be true.
Procedure
The procedure to compute the output of the neuron in the layer l is:
- Multiply the row of the weight matrix with the output of layer l-1 to get the weighted sum of inputs
- Convert the weighted sum to cumulative sum by adding the bias term of the bias vector
- Apply the activation function, to the cumulative input to get the output of the neuron in the layer l
Final Output
- Depending on the type of the problem, the output layer can have different number of neurons
- For regression, there will be a single output neuron
- For binary classification, there will be two output neurons
-
For multiclass classification, there will be as many output neurons as there are classes.
- The first neuron outputs the probability for label 1, the second neuron outputs the probability for label 2 and so on.
- The output of a feedforward network is obtained by applying the activation function on the output layer
Algorithm
-
for in
- The last layer (the output layer) is different from the rest, and it is important how we define the output layer.
- Here, since we have a multiclass classification problem (the MNIST digits between 0-9), we have used the softmax output which we had defined in the previous session:
where for and c = number of classes
This operation is often called as normalizing the vector
Complete Algorithm Steps
-
for in
Note that (the weight of the output layer) can be written as as well.
Example
Consider and and bias is 0. What will be ?
Softmax output vector (output of 3rd layer).
-
The probability order would be for the class labels
What is the predicted label?
- 2
- As the highest probability is for the neuron representing label 2, it is the predicted label.
Batch Processing
- It would inefficient to do a for loop type computation for each input row of the whole data
- We use batch processing to vectorize the process
- Small batches of the input data are created
- Each batch is processed one by one
- The calculation for the whole batch is done in one, almost as if only one data point is being fed
- Calculation is parallelized due to blockwise property of matrix multiplication
- The algorithm is similar to the one for single data point
Algorithm
-
for in :
- Note that we have used upper case H & P to denote batch processing
- and are matrices whose column represents the and vectors respectively of the data point.
- The number of columns in these 'batch matrices' is equal to the number of data points in the batch
Example
What is the dimension of the network output matrix
- There are 4 neurons in the output layer. Hence, for every input data point, there will be an output vector of shape (4,1). Since there are 50 such data points, the shape of the matrix P is (4,50).
What is the dimension of the output matrix out of the first hidden layer, that is
- There are 7 neurons in the hidden layer 1. Hence, for every input data point, there will be an output vector of shape (7,1). Since there are 50 such data points, the shape of the matrix is (7,50).
What is the dimension of the input batch
- (5, 50)
- There are 50 input data points and there are 5 neurons for each input data point. Hence, dimension = (5,50)
Takeaways
- Information flows in one direction in feed forward networks (from layer l-1 to l)
- The computation for output mostly boils down to weights * inputs + bias after which an activation function is applied
- Block matrix multiplication makes this whole process fast and paralleziable by using fast GPUs.
Questions
Consider a neural network with 5 hidden layers. Choose the ones that are correct in the feedforward scheme of things.
| Statement | True / False |
|---|---|
| The output of the 2nd hidden layer can be calculated only after the output of the 3rd hidden layer in one feed forward pass. | F |
| The output of the 3rd hidden layer can be calculated only after the output of the 2nd hidden layer in one feed forward pass. | T |
| The output of the 3rd hidden layer can be calculated only after the output of the 4th hidden layer in one feed forward pass. | F |
| The output of the 5th hidden layer can be calculated only after the output of the 2nd hidden layer in one feed forward pass. | T |
- In feed forward, output of layer 'l' can be calculated only after the calculation of the output of all the 'l-1' layer.
Consider a neural network with 5 hidden layers. You send in an input batch of 20 data points. What will be the dimension of the output matrix of the 4th hidden layer if it has 12 neurons?
- (12, 20)
- Dimension = (number of neurons in the layer, size of the batch)
Consider a neural network with 5 hidden layers. You send in an input batch of 20 data points. How will you denote the weight matrix between hidden layers 4 and 5?
- is the weight matrix between the layer l and l-1
Consider a neural network with 5 hidden layers. You send in an input batch of 20 data points. The weight matrix has the dimension (18,12). How many neurons are present in the hidden layer 2?
- 12
- Matrix dimension = (number of neurons in the layer in layer l, number of neurons in layer 'l-1')
Imagine you have a neural network in which a layer l has dimension (128, 64). How many neurons are present in layer l?
- 128
- Matrix dimension = (number of neurons in the layer in layer l, number of neurons in layer 'l-1')